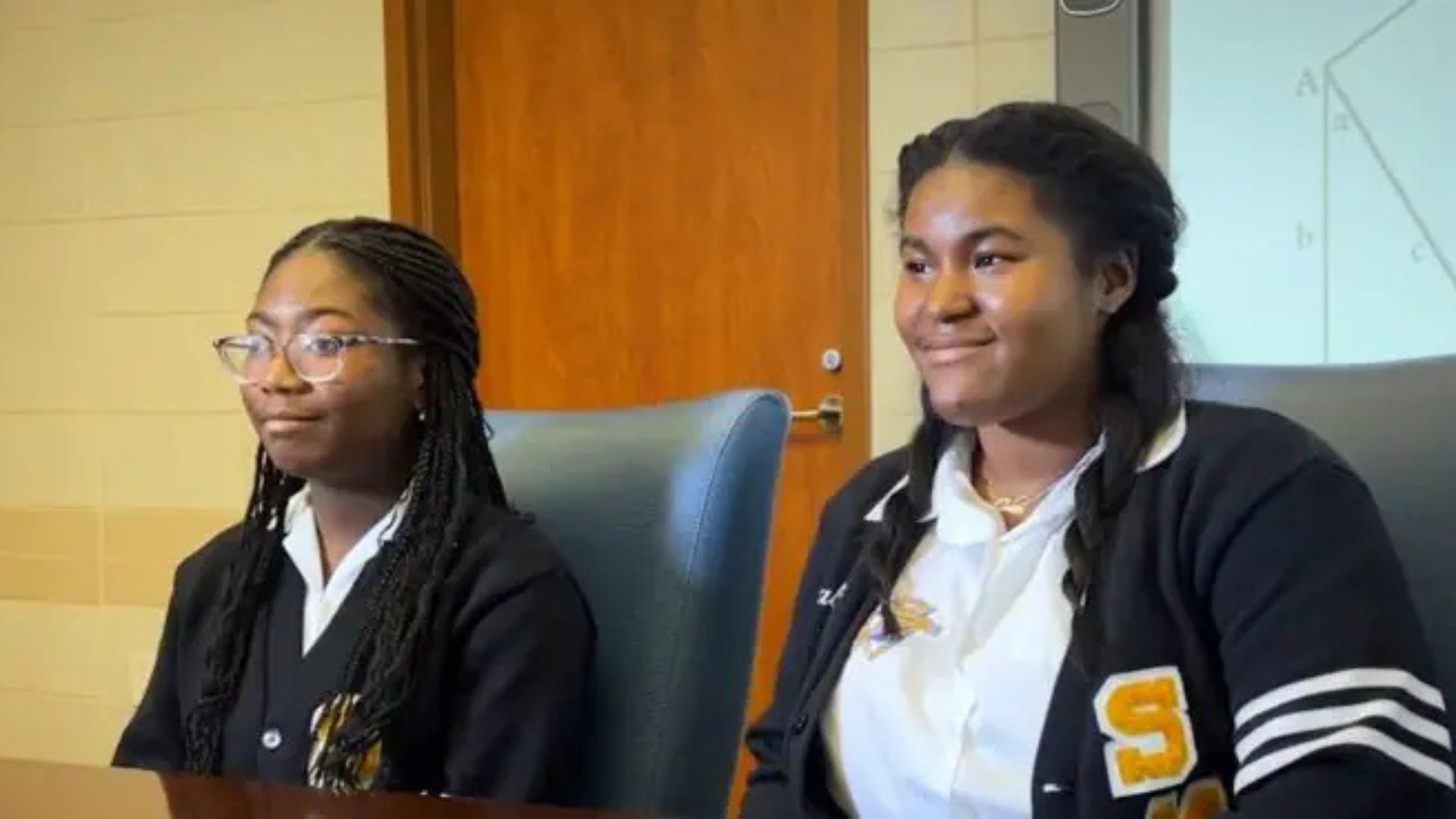
Ao longo da história, o Teorema de Pitágoras tem sido um dos pilares da matemática, conhecido principalmente pela relação a² + b² = c² em triângulos retângulos. Embora essa relação tenha sido provada por diversas técnicas, usar a trigonometria para tal propósito sempre foi algo considerado paradoxal. Isso se deve ao fato de as fórmulas trigonométricas, frequentemente, tomarem como base a validade do próprio teorema, criando um conhecido ciclo de “raciocínio circular“.
Contudo, um feito significativo, ocorrido em 2022, merece destaque. Duas estudantes do ensino médio, Calcea Johnson e Ne’Kiya Jackson, anunciaram uma maneira inovadora de provar o teorema de Pitágoras sem cair neste círculo lógico. Em 2024, elas publicaram seus achados na renomada revista American Mathematical Monthly, causando grande impacto na comunidade matemática.
Por que o Teorema de Pitágoras é importante?
O Teorema de Pitágoras não apenas facilita a determinação dos comprimentos dos lados de um triângulo retângulo, mas também atua como base para diversas aplicações em áreas como física, engenharia e computação gráfica. Sua relevância ultrapassa os limites da geometria pura, sendo um alicerce sólido em problemas reais que envolvem medidas e direções.
A abordagem tradicional para provar o teorema vai desde a álgebra até a geometria pura. No entanto, demonstrá-lo através da trigonometria, evitando o raciocínio circular, foi um verdadeiro divisor de águas. A solução de Johnson e Jackson apresentou cinco novas maneiras de provar o teorema e elucidou um mecanismo que sugere mais cinco provas, totalizando dez abordagens inéditas.
Como a trigonometria interage com o Teorema de Pitágoras?
O cerne da questão reside no fato de que a trigonometria e o teorema de Pitágoras compartilham uma interconectividade inerente. As funções trigonométricas, como seno, cosseno e tangente, dependem da relação entre os lados de um triângulo retângulo, a qual o teorema descreve. Tradicionalmente, a validação de fórmulas trigonométricas assume a verdade do teorema como dada, criando o risco de deduções circulares.
Foi aí que a inovação de Johnson e Jackson se destacou. Elas exploraram aspectos dos ângulos e as propriedades das funções trigonométricas para construir argumentos que não assumem a princípio a veracidade do teorema, evitando assim o ciclo lógico anterior. Dessa forma, suas descobertas abrem uma nova direção para estudos e provas na matemática.
Qual é o Impacto dessa Descoberta?
O trabalho das duas jovens, além de inovador no campo teórico, representa um movimento significativo em direção à diversidade e inclusão nas ciências exatas. A presença de mulheres e, especificamente, mulheres negras, nos campos STEM (sigla em inglês para Ciência, Tecnologia, Engenharia e Matemática) ainda é menor que o ideal. Assim, suas conquistas servem de inspiração para novas gerações e destacam a importância de promover oportunidades equitativas.
Leia também: Governo abre inquérito contra TikTok por suspeita de tratamento irregular de dados